What is Limestone?

Contents

Limestone is a very common sedimentary rock. We refer to it as a carbonate sedimentary rock because it’s principal component is calcium carbonate which has the chemical formula CaCO3.

Limestone is typically deposited in marine environments which means it’s formed on the bottom of a shallow sea. From the time this limestone was deposited on in toward the present in geologic time.

These environments in which the sediment is deposited are typically teeming with life and quite often limestone is fossiliferous and you can see fossils in it.

These rocks are modeled gray and white and these models are the remnants of burrows that marine animals made in this when there was still soft lime mud at the bottom of the sea.

Geologists have a very neat way of identifying limestone in the field. Calcium carbonate reacts with acids to release bubbles of carbon dioxide. So geologists typically carry a small bottle of dilute hydrochloric acid into the field.

Types of limestone

There are two types of limestone present they are as follows:

Limestone consisting mainly of animal shells:

Many animals live in the sea, rivers or lakes. In those species many of them have shells. These shells are made up of calcium carbonate (calcite and aragonite). When these animals die, their shells are leftover on the bottom of the water. Due to this these shells get accumulated to form thick deposits.

The limestones formed due to the animal shells are as follows:

Crinoidal limestone.
Fusulinid limestone.
Reefs like limestone and Shell limestone.

1.1 Crinoidal limestone:

Well crinoids might look like a plant but they are from animals. Crinoids are part of the family of Echinoderm. Which also includes sea stars, cucumbers, sea urchins, and sand dollars. When you look at the crinoids it might look like a flower or plant, but it really is an animal. It has three main parts like arms, calyx and stem.

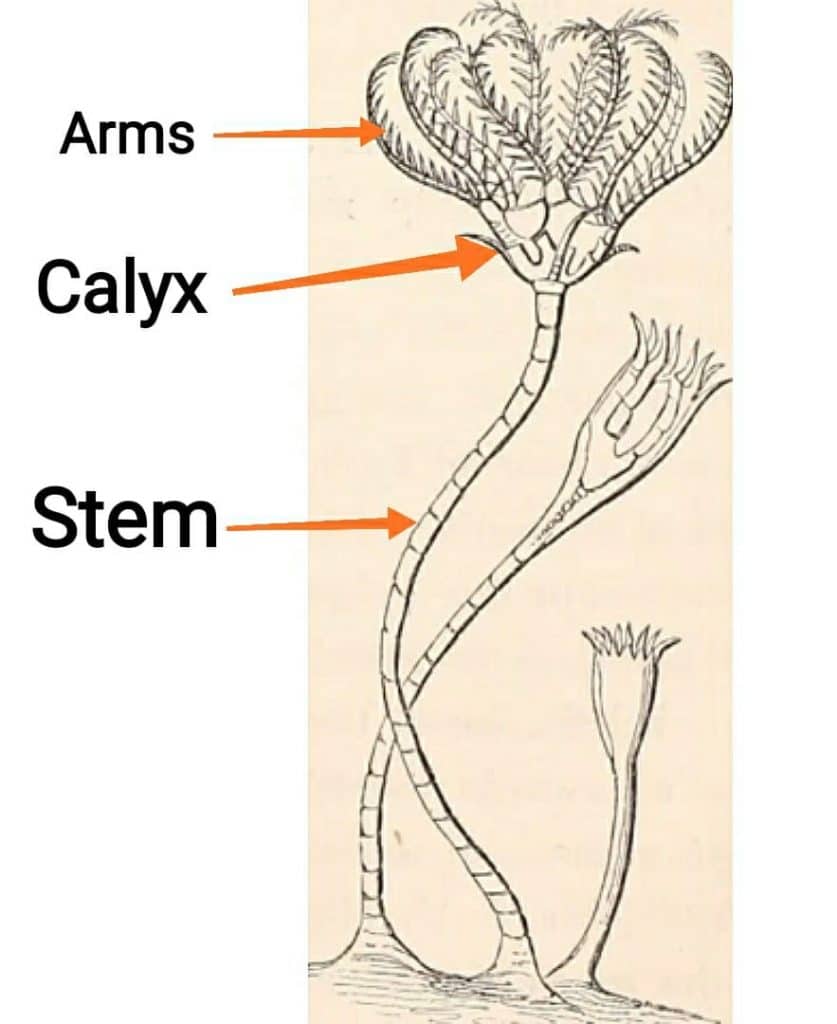
Millions of years ago the central plains of the United States all the way from the Gulf of Mexico to the great plains and into Canada, were under a very shallow part of the ocean. That’s why in certain areas around here you can actually see Crinoidal Limestone in these areas. Due to weathering action for so many years and these crinoids accumulating over and over for so many years, due to this constant process crinoidal limestone is formed.

1.2 Fusulinid limestone:

Fusulinids are the animals which are the members of the single-celled animals known as foraminifera. These animals are small in shape and their shells look like grains of wheat. They were in abundance during the Pennsylvanian and Permian periods. Many limestones are found which are mostly solid masses of fusulinids shells.

1.3 Reef like limestone and shell limestone:

These types of limestones contain the remains of brachiopods, corals, oysters, clams,bryozoans and other forms. Most of these species lived in colonies and there remains formed lens shaped or elongated deposits. These deposits grew to some several hundred miles in length. In Kansas such deposits are found but they are much smaller.

Small colonies or groups of fossil shells, when gone across such formations measured only upto a foot in diameter.

Limestones formed partly by chemical processes:

Calcium carbonate is more soluble in that water which contains carbon dioxide than in pure water. When the present carbon dioxide in the water is removed for any reason. Like plants remove carbon dioxide by using it in their food and also carbon dioxide is removed when you heat water, or when the water is evaporated in such conditions carbon dioxide is decreased. As the carbon dioxide is decreased the calcium carbonate falls out of the solution and then it settles to the bottom of the water. This calcium carbonate gets accumulated to form thick deposits.

The limestones formed by chemical processes are as follows:

Algal limestone.
Oolitic limestone.
Chalk.
Diatomaceous marl.
Travertine.
Caliche.

2.1 Algal limestone:

A kind of limestone either shaped from the remaining parts of calcium-secreting algae or framed when algae tie together the pieces of other lime-secreting living organisms.

2.2 Oolitic limestone:

Oolitic limestone is made up of small circles or orbs called otoliths. These are stuck together by lime mud. They are formed due to the deposition of calcium carbonate on the surface of sand grains when they are rolled by wave action around on a shallow sea floor.

2.3 Chalk

Chalk is soft and it is white limestone. It is made up of the remains of microscopic organisms known as coccoliths and tiny planktonic. These microscopic organisms live on the surface waters of the tropical seas.

2.4 Diatomaceous marl:

This rock is very much important because of the silica content and the calcium carbonate content from the tiny diatoms.

Diatoms are single-celled creatures that are having characteristics of both plants and animals. When these diatoms die there outer shell which is silica settles at the bottom of the lake or sea and gets accumulated. These are found in the Logan countries and Ogallala Formation of Wallace. This rock can be mined and can be used for filtering water or other solutions and also can be used as a filler in paints and other products.

2.5 Travertine:

Travertine is a combined, compact variety of limestone. It is formed at the sides of the streams, particularly near waterfalls and around hot and cold springs. Calcium carbonate is deposited, where due to evaporation of water a solution is left over. This solution is supersaturated with chemical constituents of calcite. The travertine deposit which is found near waterfalls is known as Tufa. It is a porous and cellular variety of travertine. Such deposits have been found in Butler and Riley counties.

2.6 Caliche:

Caliche is a type of sandstone and it is found from calcite that is why it is named as caliche. It is also known as calcite cemented sandstone, it is formed in the soils of dry regions. In most cases, it is impure like clay and silt, fairly soft but if the caliche is very old then they are extremely hard. This limestone is dense and it has a very distinctive structure. This limestone can be easily recognized by its pinkish color.

What is limestone used for?

We have previously learned about how limestone is formed and the limestone cycle. We will now learn about the uses of limestone and its many real-life applications. Limestone is the starting material in the production of quicklime which is calcium oxide and slaked lime which is calcium hydroxide as explained in our previous article. There are many more uses to limestone than simply producing quicklime and slaked lime.

Limestone can be used on its own, many structures have been carved out of limestone and many buildings have been built with mostly limestone. Some examples include the Empire State Building in New York, the United States of America and St. Paul’s Cathedral, and the Houses of Parliament in London England if we go further back in time.

The external structure of the Great Pyramid of Giza in Egypt is made of limestone. The walls of Machu Picchu in Peru, this shows that the usage of limestone is not a recent innovation.

There is however a fairly recent major environmental issue of acid rain that is slowly eroding these and many other limestone structures. One of the acidic components of acid rain is carbonic acid. Calcium carbonate reacts with carbonic acid to give calcium hydrogen carbonate which is soluble in water. As a result, these limestone structures erode.

Limestone can be used to make other building materials such as cement, mortar, and concrete. It can even be crushed and used as an aggregate when paving roads. The term aggregate simply refers to crushed stones and minerals for the construction of road-building purposes.

When limestone is heated with sand and sodium carbonate different types of glass can be made. Limestone can also be used to neutralize acidic waters and soil. This process is known as liming. We can mimic this liming process by placing some eggshells into a very dilute solution of hydrochloric acid. You can observe that the eggshells will dissolve in acid and gas is produced.

Finally, as limestone is white it can be crushed into a powder and this crushed powder can be used in paints and toothpaste as a coloring agent. In summary, there are many real-life applications and usages of limestone and it is not just limited to construction materials.

Lime stones can be used to help pave roads and used as a component in the formation of certain types of glass and even to neutralize acidic waters in soils.

What colour is limestone?

The limestone is found in neutral and natural colors. So when you are planning to use limestone in your house or willing to use it for the outdoor purpose, you will never have to worry about the color scheme because it practically goes with any color scheme. No matter what kind of color palette you choose limestone will always compliment it. Limestone generally varies in color like Beige, Brown, White, Blue, Green, and Grey.

Where to get limestone rocks?

The limestone rock is found in the below given places:

Marine Waters.
Caves.

Marine waters

The limestone is generally found beneath the shallow or deep marine waters. This rock is formed when organisms, skeletons of animals and calcium carbonate get combined. The shells of underwater organisms and other items build up over time and get hard on a longer scale to form limestone deposits.

These deposits are eventually so large that it is very hard to miss them. So nowadays rock and minerals companies dive into the sea and bring these limestone out and make different products out of it and utilize it in the construction activities. Every part of the limestone can be utilized and it can be placed in buildings, homes and even it is crushed and used in the construction industry.

Caves

Limestone is also formed due to evaporation in caves where water pours through the floors and sides. Because of these evaporations the calcium carbonate gets dissolved and forms deposits on the walls and ceiling of the cave. As the years pass by these deposits increase and become large in size and these also reach into the deepest parts of the cave. If they are left for many years it gets accumulated and creates mountain-like structures.

Is limestone porous?

Limestones and sandstones are very porous but some like carboniferous limestones are not at all porous but they are permeable. As limestone is highly porous so they readily absorb liquids, and they are prone to etching, and wearing away when these limestones particularly come in contact with acids.

Marble is also porous but limestone and sandstone are more porous. When limestone comes in contact with the water it absorbs the water. It is because of the pours and the texture of the limestone. So, if you ask me is limestone porous, So the answer is “yes”.

What is limestone?